Eli Peake was first here with contact juggling, then Krav Maga. Now, he brings his master thesis: An Analysis of Matrix Reduction By Columns and Its Applications to Simplicial Homology. Simplicial Homology is the study of finding holes in simplicial complexes. Each complex is a set of different lines and points due to the triangulation of an area. This can lead to many practical applications, such as triangulating hemoglobin structures and finding breakage points (holes). You can also analyze if the hole exists in some or all dimensions. According to Peake, “if a hole never dies, it persists.”
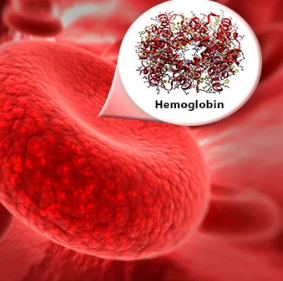
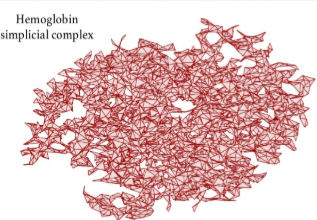
The image on the left shows hemoglobins' molecular structure. The image below shows its triangulation.
He also talked about his open-source web browser compiler, Jupyter, and basic applications of the Python code. Many were expected more of a coding based lecture; however, Peake’s project was mostly about the actual complexes. The mathematical side took up the majority of the time, analyzing what is the best way to manipulate these structures. Creating a matrix out of the points with a specified orientation, Peake shows that column reduction is the best way to find information about the homology of the complex. Using column reduction, more information can be found about the actual complex as opposed to the generally used row reduction methods. Although many were overwhelmed by how intricate his work is, the overall effect of tangible use of a computational method was beyond amazing. Peake told us “Math is my passion” before the lecture started. Despite his versatile nature, he truly loves all that he does.
Comments